AlphaFold provides high quality predictions for 3D structures of proteins based solely on amino acid sequences. The algorithm, based on deep learning methods, has excellent agreement with experimental data. The software is public and can be used by any user to predict structures [1].
Proteins are large molecules essential to all organisms. The sequence of amino acids that form a protein determines its three-dimensional structure. Each protein has a unique shape that determines its function. Being able to predict the spatial structure of a protein from its amino acid sequence has been a long-standing challenge. This task is even more challenging for proteins with a non-trivial topologies.
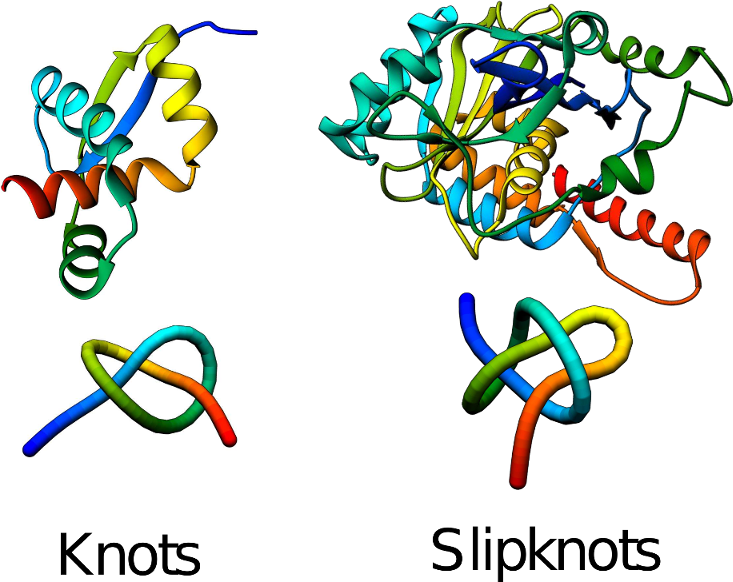
Figure 1. Example of protein with a knot (left) and with a slipknot (right). [2]
Around 2% of proteins with known experimentally-solved structures contain knots, slipknots, or links [2]. Examples of these structures are shown in Fig. 1. Our analysis of predicted structures, predicted based on the human proteome [3], has recently shown that the AlphaFold (AF2) model predicts the structure of knots in proteins with low homological models very well. Moreover, in these results, we have also found new types of protein knots (Fig. 2) and families which posses proteins with knotted and unknotted protein backbone (Fig 3.), based on [3]. Thus, AF2 can identify patterns of amino acids and network of contacts responsible for the knotting.
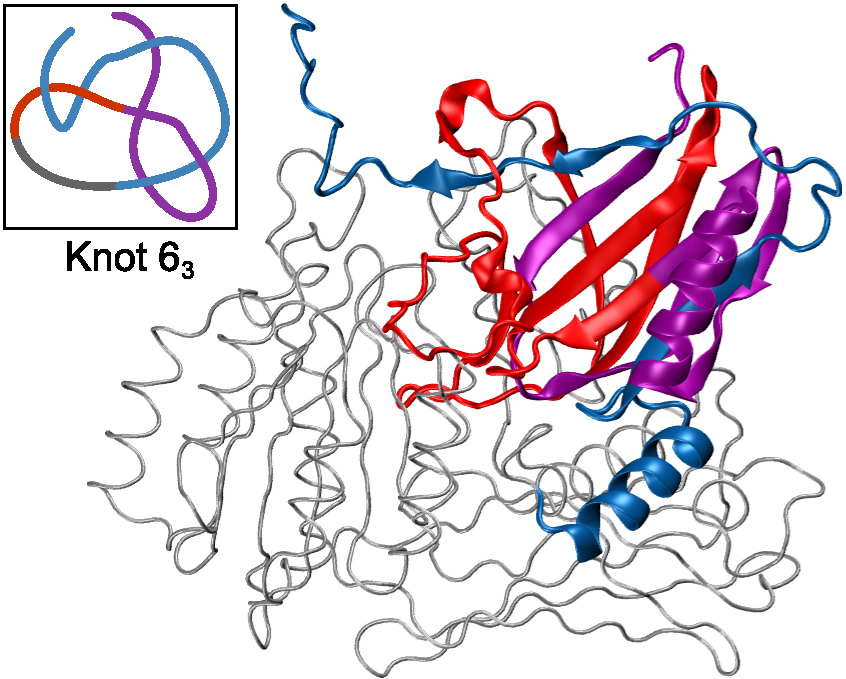
Figure 2. Protein with a 63 knot predicted by AlphaFold [3].
Herein, we present the AlphaKnot 2.0 – the first server and database to measure entanglement in AlphaFold-solved protein models while taking into account the pLDDT confidence values. AlphaKnot has two main functions: 1) providing researchers with a webserver for analyzing knotting in their own AlphaFold predictions and 2) cataloging knotting in AlphaFold predictions for which models have been published. AlphaKnot 2.0 can be used as a tool for improving the structure prediction. For example, topological differences between related proteins could reveal potential areas of improvement (or strengths and weaknesses) for AlphaFold.
AlphaKnot server provides a comprehensive topological analysis for single or multiple models uploaded in the CIF or PDB format. The results page shows the knot types, the knot pLDDT, an image matrix showing the positions of the knotted chains, a 3D manipulatable model of the protein with colored knot locations, information about the position of knots along the amino acid sequence, simplification of the protein structure, list of homologs, and other information about the protein.
The new version of the AlphaKnot database provides information about knotted structures of the whole AlphaFold database (4th version): nearly 700 K knotted proteins (with knot pLDDT >70) from over 200 million protein structures predicted by AlphaFold. Moreover, the database also contains records of ESMFold predictions for proteins with at most 400 amino acids for which AF predicted knotted structure.
Initially, AlphaKnot provided a database for all knotted structures found in the 21 proteomes (for pLDDT >50) of 1st version of AlphaFold (AF1). These knots were classified as Knots, Unsure, or Artifacts based on the pLDDT values along the subchain and visual analysis of our group. For a given protein from AF1, the page shows the same results as the server option. These data are still available in our database.
This server and database have been created in a joint collaboration between: Niemyska WH1,2, Rubach P1,3, Greń BA1, Nguyen ML1, Garstka W1, Bruno da Silva F1, Sikora M1, Jarmolińska O5. Rawdon EJ4, Sulkowska JI1
The research leading to creation of this database has been supported by: Ministry of Science and Higher Education [Idea Plus grant to J.I.S.], EMBO [EMBO YIP to J.I.S], National Science Foundation grant no. 1720342 [to E.J.R.] and COST Eutopia Action.